[Python] 인프런 강의_검정색 영역구하기(DFS)

* 인프런 강의 '입문자를 위한 코딩테스트 핵심(이론과 문제풀이) [Python]' 교안에 있는 문제입니다.

  (유료 강의 보기 바로가기)

 

---

문제 확인

 

 

 

 

 

 

 

---

 

풀이 & 배움

 

[1] 강의 정리

이 문제는 5X5 격자에서 검정색 영역들이 몇 개의 구역으로 나누어져 있는지 찾는 문제이다.

위의 필기 예시에서 구역의 개수는 2로, 2가 정답이다.

추가로 Flood fill 방식으로 DFS를 사용하여 연결된 구역을 찾는 문제이다.

Flood fill 방식은 하나의 특정한 지점에서 시작해 상하좌우로 연결된 동일한 값을 가진 영역을 모두 탐색하는 알고리즘이다.

 

크게 2중 for문을 돌아 탐색을 한다. [x, y] 기준으로  [0,0] -> [0,1] -> [0, 2] ... -> [1,0] -> [1,1] -> ... [4,4] 까지!

가다가 값이 1인 곳을 만나면(검은색으로 칠해진 곳)

4방향으로 탐색을 한다. (12시, 3시, 6시, 9시 방향)

 

위의 필기 사진을 보면, D(0, 1)에서 k = 0, 1, 2, 3 으로 나누어서

[0,1] 위치에서 12시, 3시, 6시, 9시 방향 즉, k가 0, 1, 2, 3인 곳을 확인한다.

만약 1인 값을 만나면 그 지점에서 재귀 함수를 호출해 다시 4방향 탐색을 하고,

재귀 함수가 호출될 때마다 스택 자료구조에 호출된 함수가 쌓인다.

재귀 함수 호출은 시스템 콜 스택에 쌓이므로, DFS는 재귀적으로 동작한다.

 

쌓인 함수가 다 동작되면 pop 되어 스택에서 없어지고,

빈 스택이 되면 모든 함수를 호출했으므로, 답을 반환한다.

 

 

 

[2] 코드

# 4방향 탐색을 위한 방향 벡터
d = [[-1,0], [0,1], [1,0], [0,-1]]  # 상(12시) | 우(3시) | 하(6시) | 좌(9시)

# 4방향 깊이 우선 탐색(DFS)하는 함수
def DFS(x, y, board):
    board[x][y] = 0  # 방문한 건 0으로 바꿈
    for k in range(4):  # 4방향 탐색
        dx, dy = d[k]
        nx = x + dx  # nx는 가려고 하는 지점 | k가  0이면 12시 방향의 x좌표 위치
        ny = y + dy
        
        if nx >= 0 and nx < 5 and ny >= 0 and ny < 5 and board[nx][ny] == 1:
            DFS(nx, ny, board)
        # if문 조건은 새로운 좌표가 5x5 안에 있고, 검정색(값 1)이면

# 5x5 격자를 순회하는 함수
def solution(board):
    answer = 0  # 영역의 개수    
    for i in range(5):  # 문제 요구사항 5x5 배열
        for j in range(5):
            if board[i][j] == 1:  # 최초로 1이 발견되면
                answer += 1  # 영역 하나 발견되었다고 추가
                DFS(i, j, board)  # 그 지점부터 퍼져나감
                                  # 현재 board는 solution() 함수의 지역 변수이므로 매개변수로 넘겨줘야 함
    return answer


print(solution([[0, 1, 1, 0, 0], [0, 1, 1, 0, 0], [0, 1, 0, 0, 0], [0, 0, 0, 1, 0], [0, 0, 1, 1, 0]]))
print(solution([[1, 1, 1, 0, 1], [1, 1, 1, 0, 1], [0, 0, 1, 0, 0], [1, 1, 0, 1, 0], [1, 0, 1, 0, 0]]))
print(solution([[0, 0, 1, 0, 0], [0, 1, 1, 0, 0], [0, 1, 0, 0, 0], [1, 0, 0, 1, 0], [0, 0, 1, 1, 0]]))
print(solution([[0, 0, 0, 0, 1], [0, 0, 1, 0, 0], [0, 1, 0, 1, 0], [0, 0, 0, 1, 0], [0, 0, 1, 0, 0]]))

 

 

- 코드를 작성할 때 전체 진행을 하는 함수 (진입점 solution()) 부터 작성한 후, 재귀 함수인 DFS() 함수를 작성해야 한다

 

- 탐색을 위한 방향 벡터를 전역 변수로 선언하고, 진행하는 함수와 탐색하는 함수를 적는 것은 어느 탐색이나 유사하게 진행된다

 

 

- 방향 벡터 설정 시 위와 같이 해도 되고, 아래와 같이 d를 나누어서 작성해도 된다.

dx = [-1, 0, 1, 0]
dy = [0, 1, 0, -1]

 

  단, 위와 같이 작성한다면 아래 바뀐 부분처럼 작성해야 한다.

def DFS(x, y, board):
    board[x][y] = 0  
    for k in range(4):  
        nx = x + dx[k]  # 바뀐 부분
        ny = y + dy[k]  # 바뀐 부분
        
        if nx >= 0 and nx < 5 and ny >= 0 and ny < 5 and board[nx][ny] == 1:  
            DFS(nx, ny, board)

 

 

 

동작 과정 이해하기

 

코드 이해하기

 

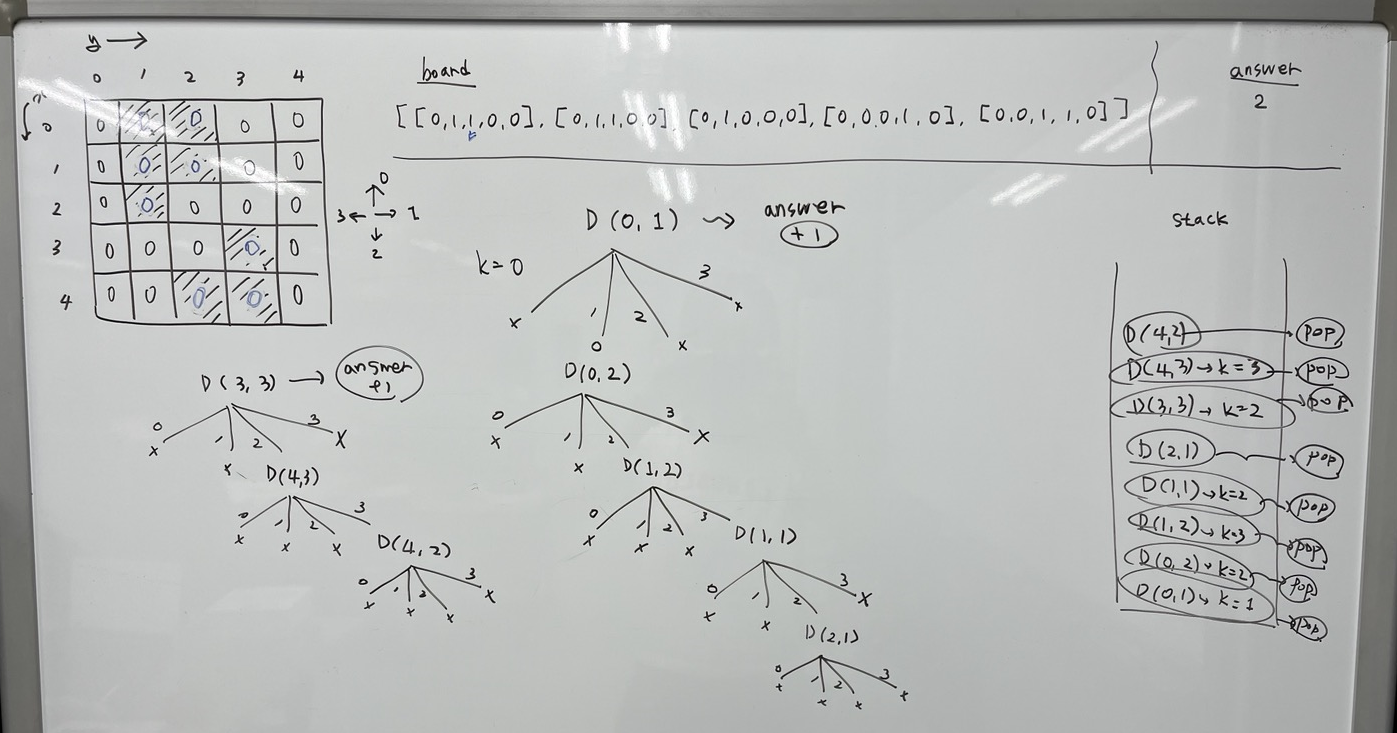
그림을 그려가며 해 보니 이해가 훨씬 수월하였습니다 :)